Calculating the radius of a circular segment

**mklotz** · May 27, 2018, 10:57 AM

The law of cosines, apparently not well known, was used in a previous post...

http://www.homemadetools.net/forum/s...-polygon-67853

to good effect to solve a not uncommon shop problem.

Here we use a somewhat more obscure theorem to unravel another shop problem.

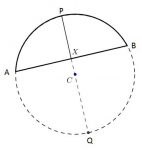
Suppose you have a circular segment like the figure APBXA in the illustration below. It could be a gear fragment, a key segment you want to reproduce, or even a flower bed you want to extend. How do you go about determining the radius of the circle from which the segment derives?

The tool we'll use is the intersecting chords theorem. It says that, if two chords intersect inside a circle, their individual parts are mathematically related to each other. A full description, including a proof of the theorem, is here...

https://en.wikipedia.org/wiki/Inters...chords_theorem

From the intersecting chords theorem, we have:

XP x XQ = XA x XB

Define:

c = AB ; c = chord length of segment
h = XP ; h = "height" of segment

which are things we can measure from the segment, then, substituting into the intersecting chords theorem, we have:

(c/2)^2 = h x XQ

which can be solved for XQ

XQ = c^2/(4h)

The diameter, PQ = PX + XQ and

PX + XQ = h + c^2/(4h) = (4h^2 + c^2)/(4h)

and the radius of the circle, CQ, is half this diameter

r = CQ = (4h^2 + c^2)/(8h)

**Imabass** · May 28, 2018, 05:03 PM

Excellent. This is common problem for buying the correct fenders for motorcycle.

**DIYer** · May 29, 2018, 06:50 AM

Thanks mklotz! We've added your Circular Segment Radius Calculation Method to our Measuring and Marking category,
as well as to your builder page: mklotz's Homemade Tools. Your receipt:

Circular Segment Radius Calculation Method by mklotz

tags: measurement

**Saltfever** · May 29, 2018, 01:02 PM

Excellent, Marv . . . keep them coming! Your timing is perfect . . . I need to extend the driveway. :-)

**mklotz** · May 31, 2018, 11:26 AM

The radius calculation here can also be used to find a circle that will pass through three (non-colinear) points.

If you have the three points identified as A, B, and P in the diagram, the calculation will, as described, find the radius of the circle that passes through those points.

Finding the center of that circle is trivial. Using the calculated radius, draw a circle around two of the points. One of the intersection points of those circles is the center of the circle passing through all three points. It should be obvious which it is but, if unsure, draw a circle around the remaining point; where all three circles intersect is the center.

**GreenSmoker** · Jun 18, 2018, 08:46 PM

Often needed for fire box to cook chamber on a smoker...

**mklotz** · Jun 19, 2018, 08:37 AM

Imabass, Saltfever and GreenSmoker

Thanks for your comments indicating that this mathematical exercise has some real utility for you.

So often, folks are completely put off by anything that even hints of math, that its utility is overlooked as they flee. Showing them that there are applications out there where it can help will encourage them to look a bit closer at the next offering.

**Tenn** · Jul 18, 2018, 07:17 PM

Originally Posted by mklotz

Imabass, Saltfever and GreenSmoker

Thanks for your comments indicating that this mathematical exercise has some real utility for you.

So often, folks are completely put off by anything that even hints of math, that its utility is overlooked as they flee. Showing them that there are applications out there where it can help will encourage them to look a bit closer at the next offering.

Well said, too often, in schools, random generic formulas ... with no practical application, confuses and frustrates otherwise willing learners. Same on the shopfloor. Often an example gives what otherwise seems like Egyptian hieroglyphs a plausible and useful application. I've had young students who said "I don't need school" change their mind when they actually saw how to apply a mathematical concept in real life. It makes all the difference in the world for many.

You can't teach what you don't know and you can't give what you don't have. ~CF