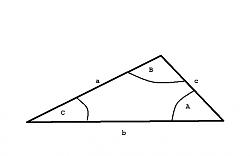
Trigonometry is all about triangles - and not just right triangles. This discussion will show you how to solve plane triangles of any type.
Any triangle has six items of information - three sides (a,b,c) and the angles opposite those sides (A,B,C). In order to solve a triangle you need to know three of those items AND AT LEAST ONE OF THEM MUST BE A SIDE. (Here "solve" means find all the unknown items.)
In the discussion that follows we will be making use of three relations that are true for ANY triangle.
Relation 1: The angles in a triangle always sum to 180 degrees.
A + B + C = 180
Relation 2: The law of cosines.
a^2 = b^2 + c^2 - 2bc * cos (A)
b^2 = a^2 + c^2 - 2ac * cos (B)
c^2 = a^2 + b^2 - 2ab * cos (C)
Aside: Note that if one of the angles is 90 degrees, cos(90) = 0 and the law of cosines reduces to the Pythagorean theorem.
Relation 3: The law of sines
sin(A) / a = sin(B) / b = sin(C) / c
There are five possible combinations for the three known items. [The triples in brackets show an example.]
SAS - Two adjacent sides and the angle between them are known [a,C,b]
SSA - Two sides and the angle opposite one of the sides is known [a,b,A]
ASA - A side and the two angles to which it connects are known [B,a,C]
AAS - Two angles and the side opposite one of the angles is known [A,B,a]
SSS - All three sides are known [a,b,c]
The technique for solving each of these possible combinations is shown; including an example using the knowns indicated in the bracketed triples above.
SAS [a,C,b]
Use the law of cosines to find the unknown side: c^2 = a^2 + b^2 - 2ab * cos (C)
Use the law of sines to find one of the unknown angles: A = arcsin [a * sin(C) / c]
Find the third angle: B = 180 - A - C
SSA [a,b,A]
Use the law of sines to find one of the unknown angles: B = arcsin [b * sin(A) / a]
Find the third angle: C = 180 - A - B
Use the law of cosines to find the unknown side: c^2 = a^2 + b^2 - 2ab * cos (C)
ASA [B,a,C]
Find the third angle: A = 180 - B - C
Use the law of sines to find the unknown sides: b = a * sin(B) / sin (A) and c = a * sin(C) / sin (A)
AAS [A,B,a]
Find the third angle: C = 180 - A - B
Use the law of sines to find the unknown sides: b = a * sin(B) / sin (A) and c = a * sin(C) / sin (A)
SSS - [a,b,c]
Use the law of cosines to find one of the angles: A = arccos[(b^2 + c^2 - a^2) / (2bc)]
Use the law of sines to find one of the unknown angles: B = arcsin [b * sin(A) / a] [could also use law of cosines]
Find the third angle: C = 180 - A - B
After you've solved your triangle, check your work. The angles should add to 180 degrees and the sides should satisfy the law of sines.
The procedures outlined here are implemented in the TRIANGLE program available on my website.


 LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks

 Reply With Quote
Reply With Quote


Bookmarks