Lathe change gears combos: Gain distribution problem.

[DIYSwede]

Cutting ordinary threads on a lathe hardly constitutes a problem with high forces thru the change gears/ leadscrew.
They're designed to hold up to that, after all.

Quite another thing happens when you want to cut steep lead ACME screws, or worms with multiple starts, right?
Then the leadscrew-to-spindle ratio could get quite a bit over unity,
as I figured out for cutting myself a 1 MOD single start worm with Pi pitch:
Hence an overdrive of 1:2,094 for my 1,5 mm/ turn leadscrew.

This ratio is ALWAYS an irrational number, as it's the result from the "DP/ Pi" or " MOD x Pi" lead/ turn.
Unfortunately real-world gears only have a rational number of teeth, so an acceptable compromise is needed.
Perhaps one of those ELS Whiz Kids out there (or Marv) will come up with an exact Pi leadscrew ratio one of these days?

This up-gearing puts quite a lot of hitherto unfelt pressure on the banjo, its gears and leadscrew ass'y (as well as on my brain).

Q: -What's the common practice regarding "change gear gain distribution" amongst machinists?

-Maybe even drive the the entire lathe thru the lead screw's rugged motor -
then perhaps there would be less stress on the gears? OTOH... Well...

Please feel free to pitch in (no pun intended) with your thoughts and experiences.


Thanks in advance.
Johan

Food for thought:



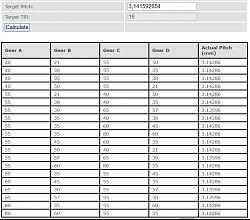
This eminent Mini Lathe change gear online calculator could be found at:
https://www.cgtk.co.uk/metalwork/ref...ears/minilathe

Note that the B & C gears are compounded on the same middle jackshaft,
so the overall gain is distributed only thru A to B, and B to C.

My intuitive thoughts are along the following lines for the alternatives in the pic above:
1) Keep all gears as big as possible throughout. (Less strain per tooth, less error)
2) Try to distribute the total gain somewhat evenly thru the two stages.
3) Prefer the bigger gain for the biggest gears. (Less strain per tooth, less error)
4) Put the biggest gain first in the chain.

Thus, given my dogmas above and available space: 60-45/55-35 may be worth a try?

[mklotz]

"This ratio is ALWAYS an irrational number, as it's the result from the "DP/ Pi" or " MOD x Pi" lead/ turn.
Unfortunately real-world gears only have a rational number of teeth, so an acceptable compromise is needed.
Perhaps one of those ELS Whiz Kids out there (or Marv) will come up with an exact Pi leadscrew ratio one of these days?"

The best rational fraction approximation to pi using integers less than 1000 is the Tsu Chung Chi approximation 355/113. Its error is something like 8.5E-6 % !!

pi = 3.1415926535898...
355/113 = 3.14159292035... (0.0000085 %)

[Aside:
Ramanujan improved on it to the point where the error is beyond the range of most calculators..
Ramanujan's improvement to Chi: (355 / 113) * (1 - 0.0003 / 3533) = 3.14159265359 (below calculator range)]

Euler's approximation...

103993 / 33102 = 3.141592653012 (-0.000000018 %)

is better but the numbers are too big to be practical for gears.

The fourth root approximation

(2143 / 22)^(1/4) = 3.14159265258 (-0.000000032 %)

provides truly astounding accuracy but is, of course, impractical for gear making.

[DIYSwede]

Thanks, Marv!
For the really discriminating, compulsory machinist perhaps this'll be good enuff:
-A pretty good approximation, (also achievable on a lathe) could perhaps be a 3-stage one:
22/17 + 37/47 + 88/83 ?

BTW: Any ideas on the "gain distribution" - should the biggest gains be put first in the chain?

Cheers